Kirchoff’s Current (KCL) and Voltage Laws (KVL)
Ohm’s
law alone is not sufficient to analyze circuits unless it is coupled with
kirchoff’s two laws:
·
Kirchoff’s
Current law (KCL)
·
Kirchoff’s
Voltage law (KVL)
KCL
KCL
states that the algebraic sum of currents entering a node (or a closed
boundary) is zero.
Where ‘N’
is the number of branches connected to the node ‘n’ is the nth
branch; and in is the nth
branch current leaving or entering a node
Convention: current entering a node is positive; while leaving a node is negative
Convention: current entering a node is positive; while leaving a node is negative

|
Alternate
KCL: The sum of currents entering a node is equal to the sum of currents
leaving the node.
Example: Write KCL on node ‘a’ and find
out ΙT.
Solution:
·
So,
an application of KCL is to combine current source in parallel into one
equivalent current source.

·
A
circuit cannot contain two different currents Ι1 and Ι2
in series unless Ι1=i2; otherwise KCL will be violated.
KVL:
KVL
states that the algebraic sum of all voltage round a closed path (or loop) is
zero.
Where M
is the no. of voltages in a loop (or number of branches in a loop), and vm
is the mth voltage.
Convention: The sign on each
voltage is the polarity of the terminal encountred first as we travel around
the loop.
Alternate
KVL: Sum of
voltage drops is equal to sum of voltage rises.
·
Note
that a circuit cannot contain two different voltage V1 and V2 in parallel
unless V1 = V2; Otherwise KVL would be violated.
Solution:
Example: Find out V1 and V2
using KVL.
We observe that answers in both examples are handled well by
polarity changes.




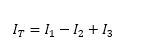











very easy to understand all math.thanks sir.
ReplyDeleteHii nice blog.
ReplyDeleteCan you give me your whatsapp number ??
Thank you very much..
ReplyDeleteYou saved me today